利用非线性散射介质进行光学加密计算和机器学习

人能透过毛玻璃等散射介质看到东西吗?按照惯例，这样的壮举被认为是不可能的。当光穿过不透明介质时，光中包含的信息变得“混乱”，几乎就像经历了复杂的加密一样。最近，IBS 分子光谱与动力学中心 (IBS CMSD) 的 Choi Wonshik 教授团队取得了一项显着的科学突破，发现了一种在光学计算和机器学习中利用这种现象的方法。

自 2010 年以来，之前的几项研究尝试利用数学方法来利用由于生物组织等散射介质而丢失的信息。这通常是通过使用光学算子(例如线性散射矩阵)来完成的，该算子可用于确定光子在经历散射时的输入-输出关系。该主题一直是 IBS CMSD Choi 教授团队的主要研究兴趣，该团队发表了许多结合基于硬件和软件的自适应光学组织成像的著作。他们的一些工作在新型显微镜中得到了展示，这种显微镜可以透过高不透明度的散射介质(例如小鼠头骨)进行观察，并对组织进行深度 3D 成像。

然而，当非线性因素加入其中时，事情就会变得更加复杂。如果散射介质产生非线性信号，则不能再简单地用线性矩阵表示，因为违反了叠加原理。此外，测量非线性输入输出特性成为一项艰巨的挑战，为研究提出了更高的要求。

揭开非线性散射介质的神秘面纱

此次，崔教授团队又取得了科学突破。他们成为第一个发现非线性散射介质的光学输入输出响应可以由三阶张量*(而不是线性矩阵)定义的人。

*三阶张量是用于表示三组数据之间关系的数学对象。简单来说，就是以三维结构排列的数字数组。张量是标量(0 阶张量)、向量(1 阶张量)和矩阵(2 阶张量)的推广，通常用于数学、物理和工程的各个领域来描述物理量及其关系。

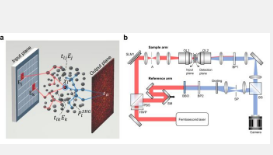
为了证明这一点，该团队使用了由钛酸钡纳米粒子组成的介质，由于钛酸钡固有的非中心对称特性，该介质会产生非线性二次谐波发生(SHG)信号。这些二次谐波信号通过二次谐波过程以输入电场的平方形式出现，当同时激活多个输入通道时会产生交叉项，从而破坏线性叠加原理。研究人员设计并通过实验验证了一种新颖的理论框架，涉及三阶张量中的这些交叉项。

为了说明这一点，研究人员通过隔离两个输入通道同时激活和每个通道单独激活时产生的输出电场之间的差异来测量交叉项。即使只有 49 个输入通道，也需要通过两个独立输入通道的可能组合来设置额外的 1,176 个测量值。

“从弱非线性信号中检测交叉项所需的工作量非常大，”该研究的主要作者 MOON Jungho 博士指出。

释放现实世界的应用

从非线性散射介质导出的张量比线性散射介质的矩阵具有更高的秩，暗示其作为可扩展物理算子的潜力。该团队通过非线性光学加密和全光逻辑门的实际实现证明了这一点。

首先，该团队成功证明了非线性散射介质可用于光学加密过程。当特定图像信息输入到介质中时，输出的二次谐波信号会显示为随机图案，类似于一系列加密过程。相反，通过对二次谐波的三阶张量表示进行逆运算，可以通过解密过程恢复原始输入信息。利用张量输入输出响应的逆运算，他们从随机编码的 SHG 信号中解码出原始信号，这比使用线性散射介质的标准光学加密提供了增强的安全性。

此外，数字相位共轭的集成使研究人员能够展示仅当两个特定输入通道同时激活时才激活的全光与逻辑门。与硅基逻辑相比，这种方法具有潜在优势，包括降低能耗和光速并行处理能力。

这项研究有望开辟光学计算和机器学习领域的新领域。“在新兴的全光学机器学习领域，非线性光学层是增强模型性能的关键。我们目前正在研究如何将我们的研究整合到这一领域。”Choi 教授说道。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！