科学家提出基于机动参数估计的空间非合作目标轨迹跟踪研究

首先，作者简要描述了跟踪非合作空间目标机动轨迹的两种模型：相对动力学模型和间接测量模型。在相对动力学模型中，跟踪目标的机动轨迹被建模为在短离散时间间隔内跟踪目标位置的问题。另一方面，间接测量模型将雷达得出的值直接转换为局部垂直局部水平 (LVLH) 坐标系中的测量结果。

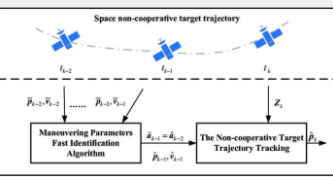
接下来，针对复杂机动模型、高频观测的目标跟踪问题，提出一种基于非合作目标参数估计快速估计的实时机动轨迹跟踪方法。轨迹跟踪算法框图。如图2所示。通过在高频观测时选择离散节点t k − 2、t k − 1和t k，实时获得非合作目标的相对位置和速度。在每个节点，利用历史观测数据和机动参数估计，算法预测目标在下一个节点 t k的相对位置 p k。假设机动参数在离散化周期内保持不变，从而允许在 t k − 1处获得完整的相对状态信息。离散轨迹跟踪算法通过预测目标位置来跟踪机动轨迹。这个过程在不同的节点重复进行，实现基于测量数据的连续机动轨迹的有效跟踪。然而，历史测量误差会影响目标加速度的识别。为了减轻测量误差对目标加速度识别的影响，采用均值滤波方法对t k - 2到t k - 1期间的历史测量进行平滑。考虑到非合作目标机动参数满足三轴加速度约束，采用射击方法生成机动参数估计，以保证约束范围内的均匀分布。通过数值积分得到t k − 1时刻目标的相对状态。采用微分代数方法解决了蒙特卡罗方法的计算负担，保证了实时跟踪过程的效率。机动参数快速识别算法流程如图3所示。该方法首先选择标称状态X 1k−2，并将相关的状态偏差定义为△x，其中每个状态都可以通过在标称状态上加上偏差值来描述。然后，在标称状态X 1k-2附近执行泰勒展开。利用龙格-库塔积分器，将时间 t k − 2处的状态映射到 t k − 1，从而得到半解析多项式解 [X ik−1 ]。通过比较估计值和测量值的误差，得到最佳估计状态X k-1 。最后得到最优估计值a k−2目标从t k − 2到t k − 1的机动参数是通过X k−1 [ key ] 得到的。整个过程通过Jet Transport算法进行多项式数值计算，保证实时跟踪时减少计算负担。

此外，空间非合作目标离散轨迹跟踪算法流程如图4所示。考虑到非合作目标的轨迹离散化周期间隔较短，假设连续2个周期内目标的机动参数相等。因此，通过求解方程组，即可得到目标的相对状态x k − 1 。利用状态转移矩阵F和参数θ，计算出目标在t k时刻的相对状态x k，实现对目标的轨迹跟踪。

接下来，为了评估算法的性能，作者进行了非合作目标跟踪仿真，并与交互式多模型方法(IMM)相比，分析了该方法的跟踪误差和时间成本。仿真条件包括非合作目标的轨道参数和初始相对状态，使用机载雷达传感器测量模型的离散轨迹跟踪周期为0.5秒。将均值为零的高斯白噪声设置为测量噪声，并考虑 2000 个加速镜头。IMM算法应用两个模型，在相同条件下进行200组重复实验。

将非合作目标的机动轨迹分为三个阶段并在LVLH坐标系下进行仿真，包括真实轨迹和实测轨迹。结果表明，所提算法在轨迹跟踪精度方面较IMM算法具有显着优势。位置估计的均方根误差(RMSE)表明，所提出的算法在所有三个方向上的性能均明显优于IMM算法。三轴位置估计的平均 RMSE 分别增加了 94.37%、93.53% 和 93.75%，如表 2 所示。此外，图 7 展示了所提出的算法在加速度估计方面的优越性能。此外，作者对仿真结果进行了详细分析，包括位置估计的平均均方根误差、目标加速度估计的性能以及算法的运行时间。实验表明，该方法不仅具有优异的跟踪性能，而且满足实时机动轨迹跟踪的约束，尽管与IMM算法相比计算成本较高。综上所述，对于机动频率高的非合作目标，该算法在机动跟踪问题上表现出更好的性能。

总之，作者总结了他们的工作，并强调了研究的两个创新点：(a)他们提出了一种基于微分代数方法的快速目标机动加速度估计方法，避免了传统滤波算法对大机动目标轨迹的延迟响应。与IMM方法相比，该算法能够更准确地估计目标的机动加速度，更接近目标的实际机动过程。(二)。该方法通过轨迹离散化、快速机动参数估计和轨迹预测来实现目标跟踪。与IMM相比，所提出的算法更加准确，轨迹跟踪精度提高了约93.07%。

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！